说明:对于想要入门大模型的小白,RNN作为NLP的基础一定得要好好学啦,让我们一起学习RNN叭!
目录
首先,让我们了解一下序列是什么。序列在深度学习中一般指的是带有时间先后顺序(拥有逻辑结构)的一段具有连续关系的数据(例如文本,语音等)。下图展示了一些常见的序列信息:
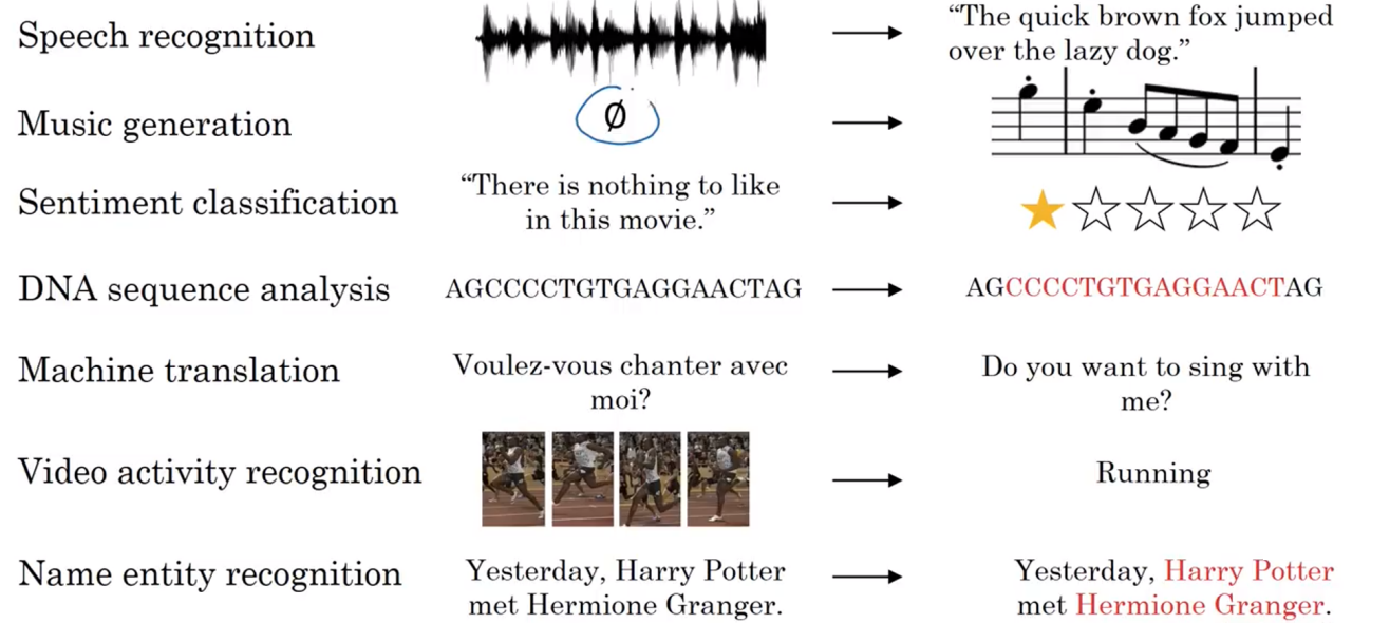
由此可见,序列可以应用在众多领域,包括但不限于:语音识别、音乐发生器、情感分析、DNA序列分析、机器翻译、视频动作识别和命名实体识别…
在NLP任务中,一般都是Seq2Seq(Sequence to Sequence)的任务。但是,传统神经网络每一层是相互独立的,同一层中每个节点之间也是相互独立的,因此传统神经网络无法共享输入序列之间的特征。并且,不同样本的输入序列长度和输出序列长度不同,造成传统神经网络很难做到全部统一。解决办法之一是设定一个最大序列长度,对每个输入和输出序列补零并统一到最大长度。但是这种做法实际效果并不理想。
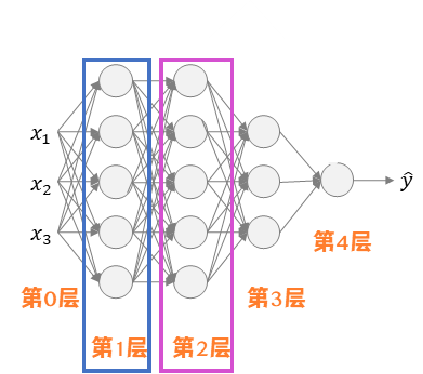
但是,RNN可以很好解决上述问题。RNN很擅长根据上文信息,对接下来的词进行推理(就比如“我要吃…”,按照语法规则,后面接上名词的概率比较大。如果后面再出现动词的话,就大概率不符合语言逻辑的),因此能够很好地共享输入序列之间的特征。并且,RNN的架构也十分灵活(这一部分我会在后面详细介绍哈~),所以处理任意长度的输入序列和输出序列都是十分轻松的!
二、RNN的架构
那么RNN的架构长什么样呢?下图展示了RNN的一般架构:
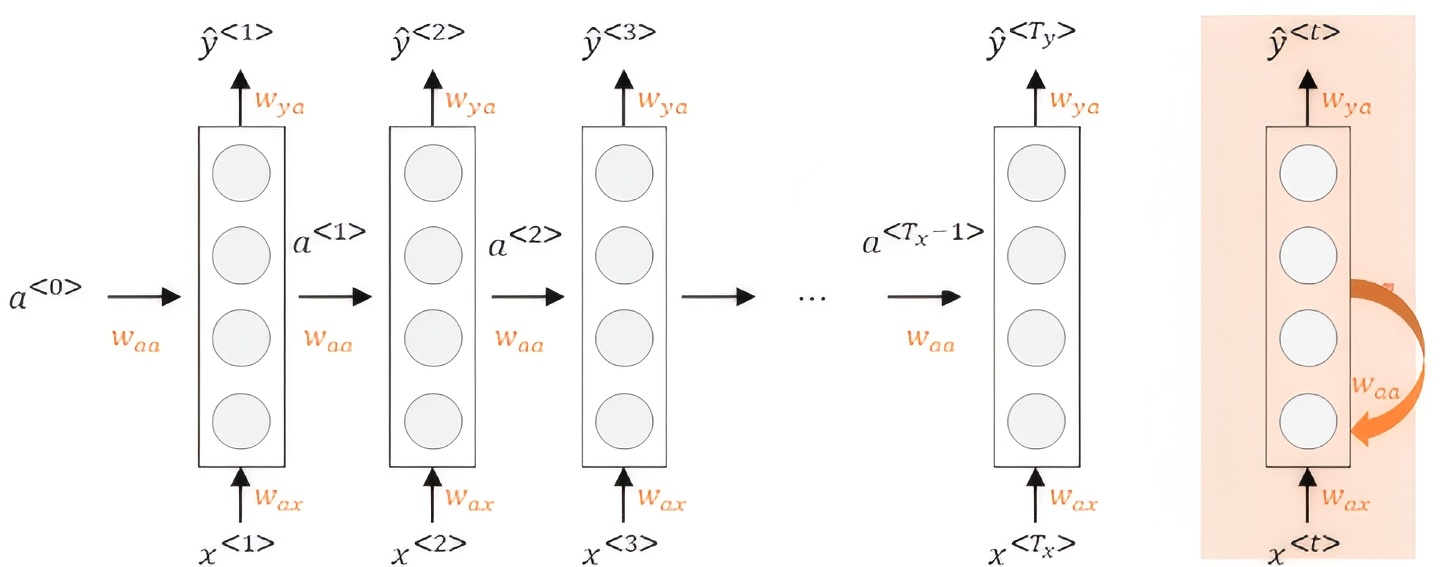
其中 $a^{<0>}$ 一般都是零向量。那么以 $t=1$ 为例,具体的计算流程如下:
\[a^{<1>}=g_1(W_{aa} \cdot a^{<0>}+W_{ax} \cdot x^{<1>}+b_a)\]其中,激活函数一般会选择使用 $tanh$ 或 $ReLu$ 。
\[\hat{y}^{<1>}=g_2(W_{ya} \cdot a^{<1>}+b_y)\]其中,激活函数一般会选择使用 $Sigmoid$ 。
那么推广到 $t$ ,公式就是这样啦:
\[a^{<t>}=g(W_{aa} \cdot a^{<t-1>}+W_{ax} \cdot x^{<t>}+b_a)\] \[\hat{y}^{<t>}=g(W_{ya} \cdot a^{<t>}+b_y)\]那么为了简化表达式,可以对 $a^{t}$ 项进行整合:将 $W_{aa}$ 和 $W_{ax}$ 水平排列为一个矩阵 $W_a$ ,同时将 $a^{t-1}$ 和 $x^{t}$ 堆叠成一个矩阵,则有:
(Bug:这里的行内公式的 $t$ 或者 $t-1$ 都需要带上尖括号 “<>”,这里的尖括号代表的是时间步 $t$ ,但是由于有Bug,就没有带了哈…)
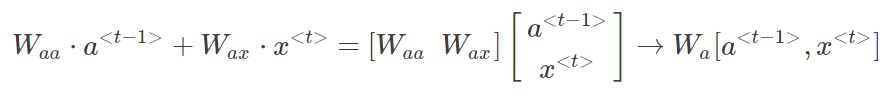
大致的RNN架构就像上面所述,值得一提的是,上面的RNN准确说是单向的RNN(left-to-right),因此 时间步 $t$ 时刻的 $\hat{y}$ 只与左边 $t-1$ 的元素有关,但是有时候也与右边的元素有关,因此后面会讲到双向RNN,简称为BRNN。
三、通过时间反向传播
为了计算反向传播过程,在单个时间步上某个单词预测值的损失函数采用交叉熵损失函数,单个元素的 $Loss \quad function$ 如下所示:
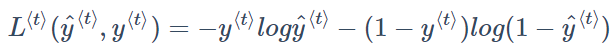
将单个位置上的损失函数相加,得到该样本所有元素的 $Loss \quad function$ 为:
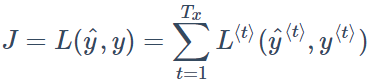
RNN的反向传播又被称为通过时间反向传播(Backpropagation through time),从右向左的计算就像是时间倒流,其过程就是在求偏导数,思路与传统神经网络一致。下图展示了更加详细的计算过程:
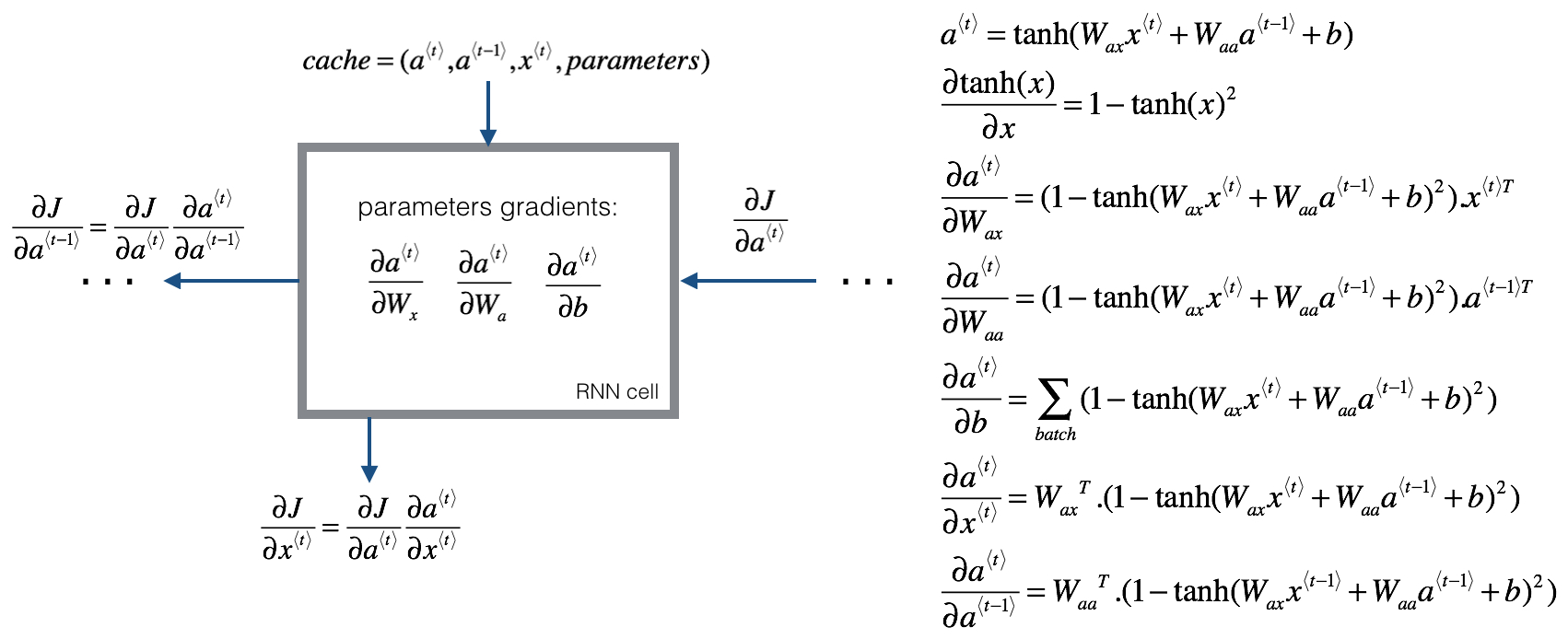
四、RNN的多种架构
由于输入序列和输出序列的长度并不一致。因此,根据所需的输入序列和输出序列长度,可以将网络分为:
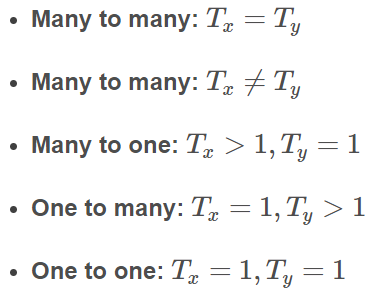
不同类别的结构示意图如下:
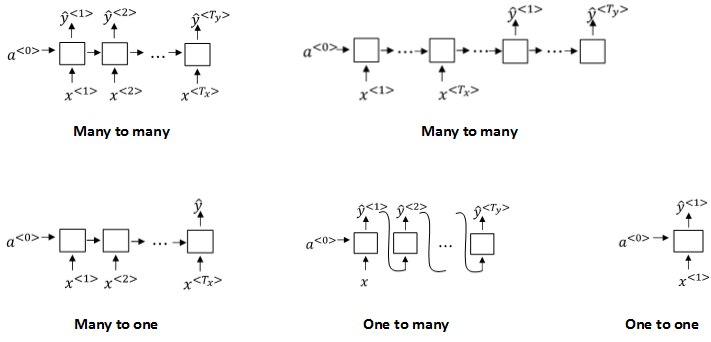
其中,第二种Many to Many的架构值得关注下,因为这便是Encoder-Decoder架构的雏形。
五、梯度消失问题
但是,RNN真的那么好用吗?我们可以看下图出现的情况:
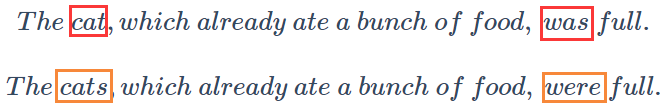
这两句话中:was受到cat影响,were受到cats影响。它们之间跨越了很多单词,而RNN模型每个元素受其周围元素的影响较大,所以难以建立跨度较大的依赖性。所以普通的RNN面对上面这两句话很容易出现梯度消失的情况,很难捕捉它们之间的错误,造成语法错误。
那么究其原因,我们可以回到第三部分介绍到的通过时间反向传播,本质就是在对 $W_x$ 、 $W_s$ 、 $W_o$ 以及 $b_1$ 、 $b_2$ 求偏导,并不断调整 $L$ 使其尽可能小。 对 $W_o$ 求偏导是没问题的,但是对 $W_x$ 、 $W_s$ 求偏导是有着长期依赖的问题,具体公式见下图:
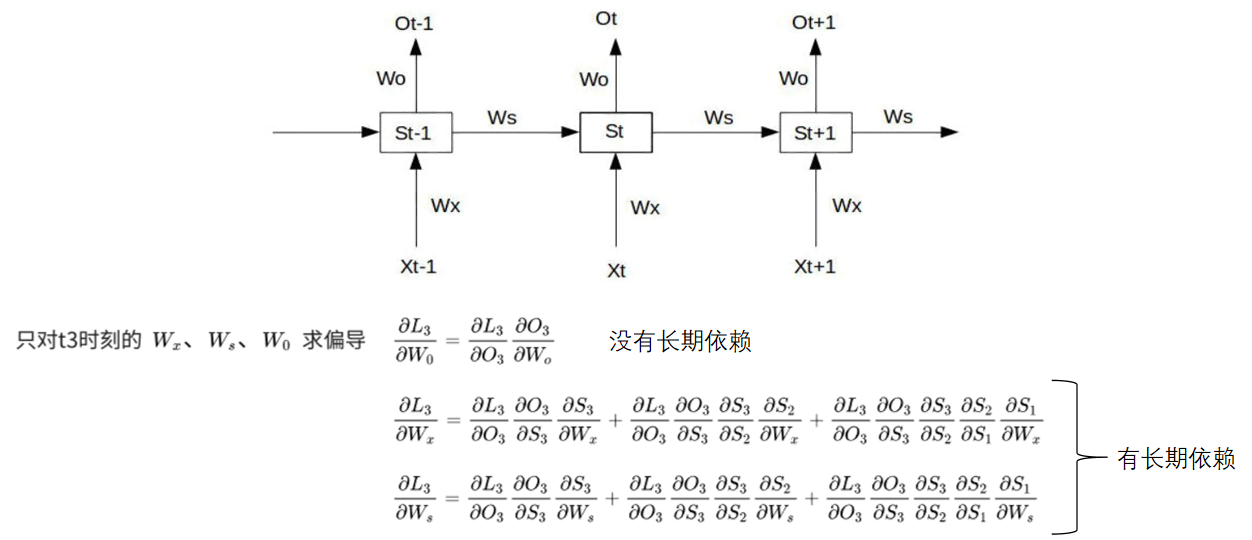
我们以 $W_x$ 为例,进一步理解梯度消失的出现:
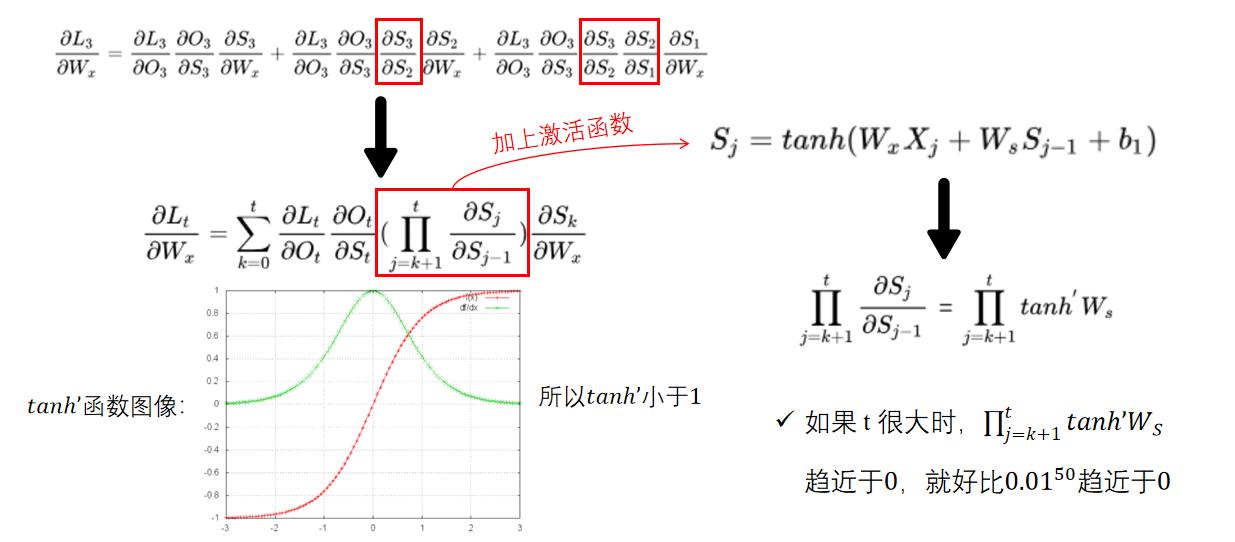
六、残差网络
面对梯度消失的问题,或许残差网络是个解决梯度消失问题的不错思路。残差网络离不开残差块,因此下图展示了残差块的结构:
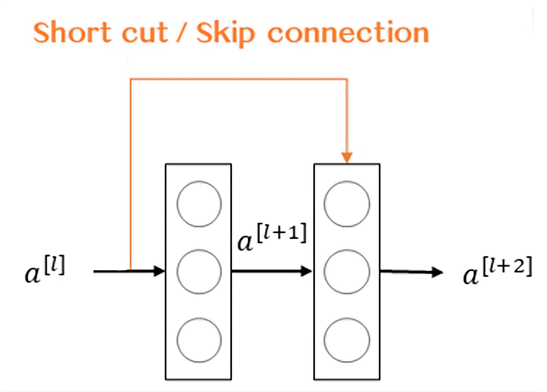
残差块通过捷径(Short cut或Skip connections) 将 $a^{[l]}$ 与 $a^{[l+2]}$ 之间的隔层联系。表达式如下:
\[z^{[l+1]}=W^{[l+1]} \cdot a^{[l]}+b^{[l+1]}\] \[a^{[l+1]}=g(z^{[l+1]})\] \[z^{[l+2]}=W^{[l+2]} \cdot a^{[l+1]}+b^{[l+2]}\] \[a^{[l+2]}=g(z^{[l+2]}+a^{[l]})\]构建一个残差网络就是将众多的残差块堆积在一起,形成一个深度网络。其网络架构如下:
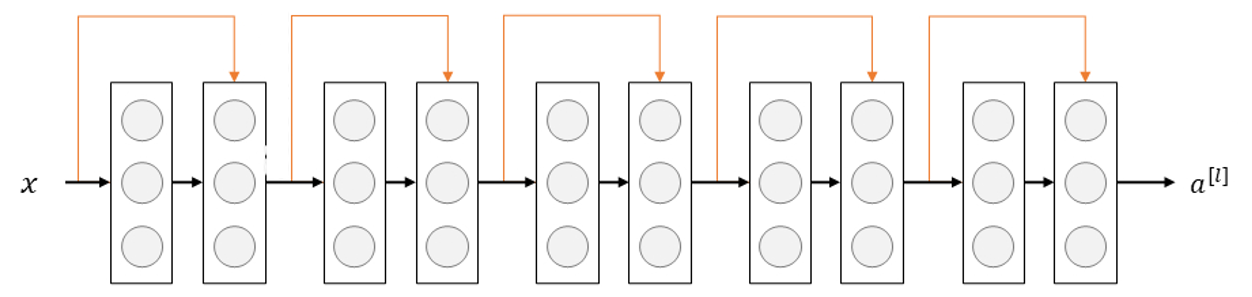
理论上,随着网络深度的增加,模型学习能力变强,效果应该提升。但实际上,如下图所示,一个普通直连网络,随着神经网络层数增加,训练错误会先先减少后增多(称之为网络退化/梯度消失)。但使用跳接的残差网络,随着网络变深,训练集误差持续呈现下降趋势。
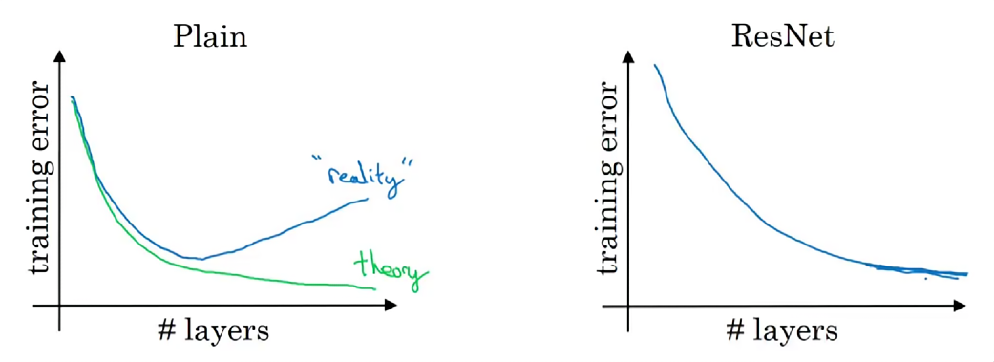
残差网络有助于解决梯度消失和梯度爆炸问题,使得在训练更深的网络的同时,又能保证良好的性能。
那么为什么残差网络是有效的呢?下面将基于一个例子来解释为什么ResNets有效。
假设输入 $x$ 经过很多层神经网络后输入 $a^{[l]}$ , $a^{[l]}$ 经过一个残差块输出 $a^{[l+2]}$ 。 $a^{[l+2]}$ 的表达式如下:
\[a^{[l+2]}=g(z^{[l+2]}+a^{[l]})=g(W^{[l+2]} \cdot a^{[l+1]}+b^{[l+2]}+a^{[l]})\]输入 $x$经过很多层神经网络后,若 $W^{[l+2]}≈0,b^{[l+2]}≈0$ ,则有:
\[a^{[l+2]}=g(a^{[l]})=ReLU(a^{[l]})=a^{[l]}\] \[when \quad a^{[l]} \geq 0\]上面的公式表明,即使发生了梯度消失 ($W^{[l+2]}≈0,b^{[l+2]}≈0$),也能够直接建立 $a^{[l+2]}$ 与 $a^{[l]}$ 的线性关系:$a^{[l+2]}=a^{[l]}$。当然,如果没有发生梯度消失时,残差块会忽略short cut,从而达到同样效果的非线性关系。
七、GRU(门控循环单元)
GRU(Gated Recurrent Units, 门控循环单元) 改善了RNN的隐藏层,使其更好地捕捉了深层连接,并改善了梯度消失的问题。
GRU有一个新的变量称为c,代表记忆细胞(Memory Cell),其作用是提供记忆的能力,记住前文的一些重要信息(如:是单数还是复数),在时间 $t$ ,记忆细胞的值 $c^t$等于输出的激活值 $a^t$ 。具体的相关公式如下:
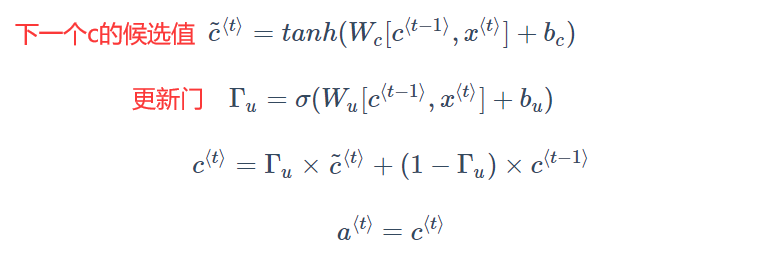
添加了记忆单元之后的结构如下图所示:
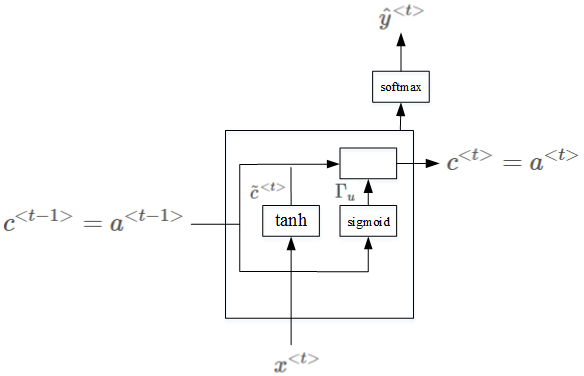
当使用Sigmoid作为激活函数得到更新门的值时候,更新门的值在0-1的范围内,且大多数时候非常接近0或1。当更新门的值等于1时,表示记忆细胞 $c$ 需要更新,等于0的时候则保持不变。因此,在很长的序列后, $c$ 的值仍然能够被维持,从而实现了“记忆的功能”。

上面是被简化后的GRU单元,但是蕴含了其最重要的思想。完整的GRU还有一个相关门(Relevance Gate),代表 $\tilde{c}^t$ 和 $c^t$ 之间的相关性。因此,表达式需要修改为:
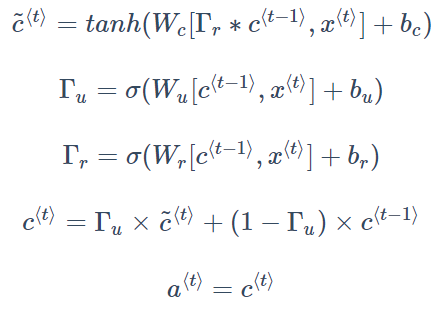
八、LSTM(长短期记忆)
LSTM(Long Short Term Memory,长短期记忆)网络比 GRU 更加灵活和强大,它额外引入了遗忘门(Forget Gate) 和输出门(Output Gate)。
LSTM是另一种更强大的解决梯度消失问题的方法。它对应的RNN隐藏层单元结构如下图所示:
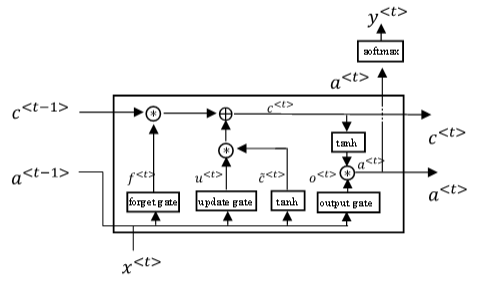
其结构图和公式如下:
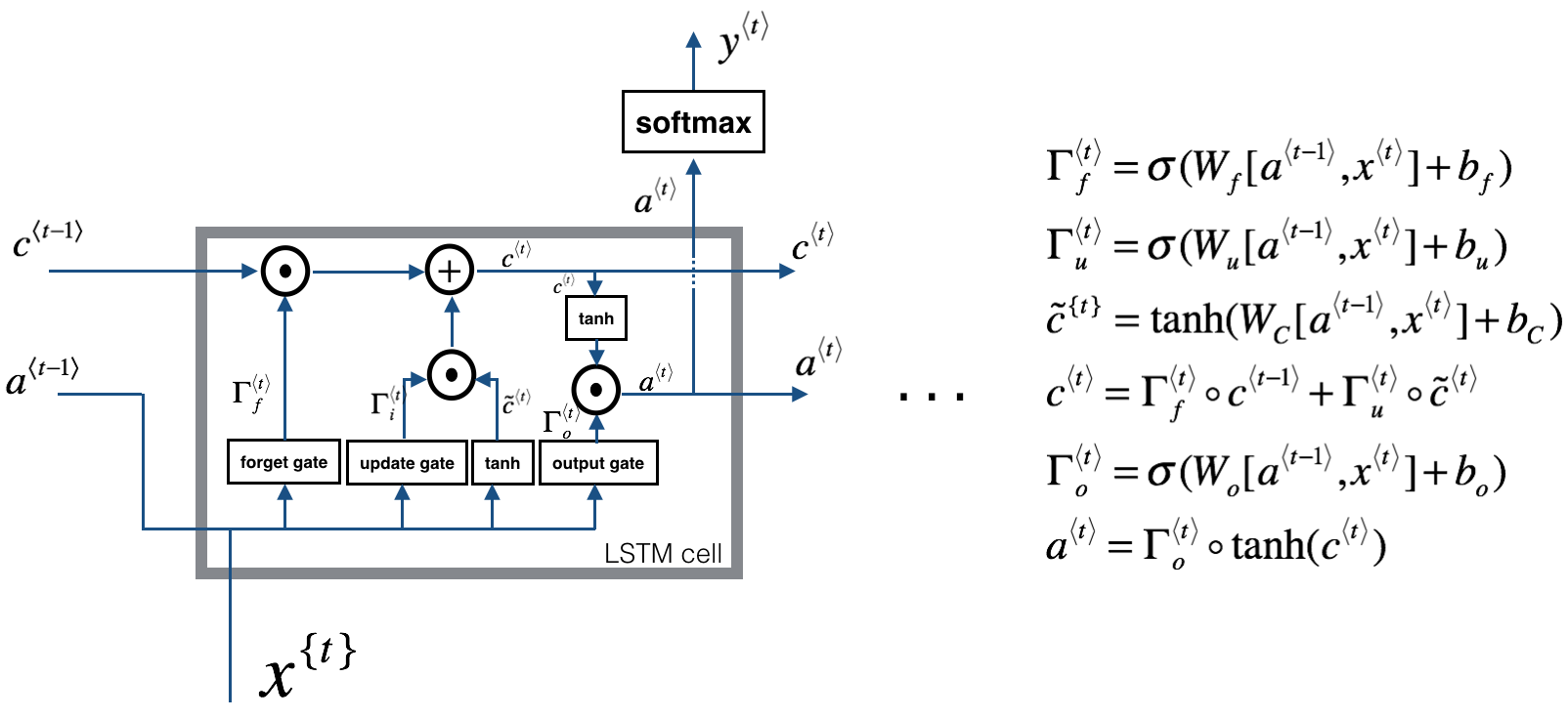
由于RNN、GRU、LSTM现在已经很OUT了,所以也不再赘述哈,有兴趣的可以自行网上搜索!
感谢阅读!如果有任何疑问,可以与俺邮箱联系哦😊